数据库加密方法可以应用于不同的环境中,但存在一个共同的问题。为此,基于复合同态的数学理论基础,提出了美复合同态的概念,并将其应用于实现浮点数据的同态加密机制。
一、秘密同态及其整数实现。
秘密同态是由Rivest等人在78年内提出的,允许直接操作密文的加密变换。然而,由于它对自己的知识文本的攻击是不安全的,Domingo进一步改进了它。秘密同态技术最早用于加密统计数据,由算法同态,确保用户可以操作敏感数据而不泄露数据信息。秘密同态技术是基于代数理论的,其基本思想如下:
设置EK1.DK2分别代表加解密函数。明文数据空间中的元素不能操作形成的密文数据库。它是一个有限的集合{M1,M2..,mn}。α和β代表操作,如果1。
函数族(EK1、EK2、α和β)是一个秘密同态。
算法实现过程如下:
选择安全大素数p.g,并计算m=pq(m保密)。
选择安全参数n(根据需要选择合适的尺寸)。
c)明文空间T=Zn(小于Z的所有非负整数集合),密文空间1。
d)选择两素数rp.,rq,分别满足rpeZP、rqzq。
确定加密密钥为K=(p、g.rp、ry)o。
f)加密算法:x.Zn,配有一明文算,随机将x石分为n份:x1、x2、x2、xn,并满足。
![]()
二、类复合同态基本运算。
类复合同态操作完成了浮点数的同态加密过程,也是本部分的核心。以下基本操作包括上述浮点数到整数的同态转换EKL(x)和整数的同态加密算法EK2(x)。
实现过程如下:
A)类复合同态的加减法操作。
![]()
b)类复合同态的乘法运算。
![]()
c)类复合同态的除法操作。

也就是说,类复合同态加密后获得的密文之间的加减乘除操作相当于明文基本操作后的加密。以下是浮点数加密操作的两个例子。使用的数据有点小,但可以反映基本的加密过程(为了清晰简单,在加密过程中将中间生成的整数分成两部分进行操作)。
例1加法操作:设置加密钥p=17、q=13、rp=2、rq=3、明文x1=0.3、X2=-0、1、X3=20。
类复合同态的加密原理,设置k=l,则有:
![]()
则有:
![]()
解密计算结果。
![]()
例2乘法操作:令加密钥p=17,q=13,rp=2,rq=3,明文x1=0.03,X2=0.10。
类复合同态的加密原理,设置K=2
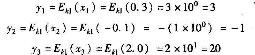
则有
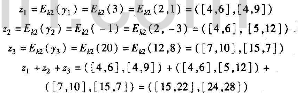
解密计算结果。
![]()
4.安全分析。
将同态加密机制的应用从整数扩展到浮点数范围,使秘密同态加密算法更加实用。即使在Eki(x)加密转换后获得相同的数据,由于第二次同态加密素数的随机选择和加密数据的随机分割,所获得的加密数据也是不同的。浮点数同态加密保留了外层加密中原始秘密同态加密的安全性,同时也对原始数据进行了双重同态转换,安全性只差。浮点数上的同态加密机制在安全性方面也能抵知密文攻击和已知文攻击。
三、字符串数据的同态加密。
与整数不同的是,在整数加密后可以实现的加、减、乘。除了操作对字符串没有意义,因此本文通过中国剩余定理转换字符串,然后使用秘密同态算法进行加密。具体算法如下;
a)设置一个字符串B,将字符串中的每个字符取其ASCII码,分别表示为bi、b2...bk:其中k是字符串中的字符数。
b)对应于两个互素的正整数,设为m1、m2、mk(mi≥121)。
c)由中国剩余定理得同余式组。
![]()
d)同余式组的解1是要加密的整数值。
E)根据秘密同态算法解密后可以得到加密数据x,则由6i=xmodmi;可以得到字符串中每个字符对应的ASCII码值。
使用中国剩余定理的证明方法来证明字符串与加密整数值之间的对应关系。在具体实现过程中,素数的选择和存储也是一个需要考虑的问题。在安全性方面,它仍然保留了原始整数秘密同态加密的特点。
中国小知识剩余定理。
在中国古代,同余式组(见同余)是一种重要的定理。