月犬云盾 原宏杰加密

基于耦合图像格子的分组图像加解密。

复合密码结构的安全性能强度优于简单的密码结构，因为复合密码结构采用循环迭代结构交替使用置乱和置换等基本操作，使密码具有更好的安全性。

根据耦合图像网格，可以设计基于分组密码和循环迭代结构的数字图像加密算法。以Kn为子钥匙，L和T分别表示TCML的空间和时间参数，Ln和RN分别表示图像的左右部分。

步骤1：初始替换原始图像（设置为M×N）并获得图像P。本文采用量化的标志混沌序列与原始图像不同或实现初始替换。

步骤2:划分更换后的图像P，将图像分为左右两部分，记录为L0和R0。

步骤3：以K1为子钥匙，使L=M、T=N/2产生M×(N/2)TCML矩阵V。

步骤4:用矩阵V构建S盒[12-13]，选择V中的混沌序列{a11，a12..，a1(N/2)，a21..，AM(N/2)}，逐行(列)中的元素进行升降序列，得到矩阵V1。确定矩阵V的每个元素在V1中的位置，形成替换矩阵S。

步骤5：用S盒替换R0，替换结果与L0不同或计算。得到的结果是下一轮迭代计算的L1，下一轮迭代计算的R1直接取L0。

步骤6：使用K2、K3。。。Kn作为子钥匙，重复步骤3至步骤5。步骤7结合最终迭代计算结果，Ln和Rn获得图像P'，并向替换P'与步骤1相反（IP-1）。获得最终图像Q是密文图像。



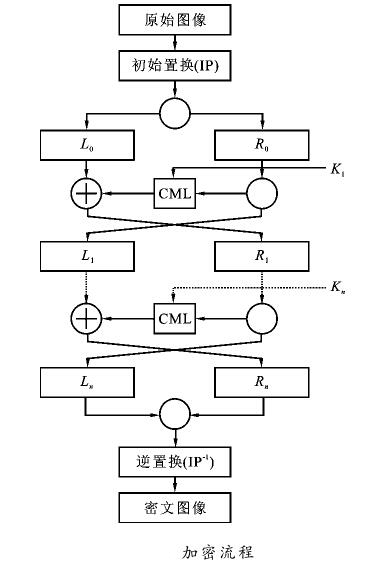
在上述算法中，初始替换和反置换的作用是扩散原始图像的灰度值，以抵抗已知的明文攻击。由于基于耦合图像网格的分组密码和循环迭代结构，设计的加密过程可以有效地抵抗差异攻击。

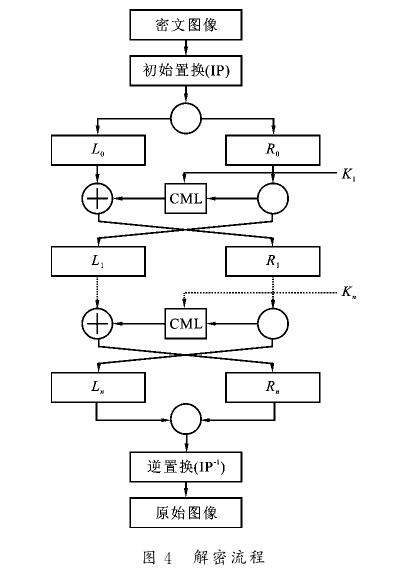
解密过程与加密过程结构一致，只需将子密钥序列倒序输入即可获得解密图像。具体的解密过程如图所示。



相关性分析

由于图像相邻像素的灰度值具有较强的相关性，因此原始图像相邻两个像素之间的相关性较高。由于密文图像的余度分散到每个像素点，因此相邻两个像素之间的相关性将大大降低。原始图像的相关系数远远超过密文图像的相关系数，这表明新算法具有良好的冗余扩散性。

将分组密码中的循环迭代结构应用于图像加密算法的设计构，并设计了一种基于耦合图像网格的分组图像加密算法。由于每轮加密采用不同的耦合图像网格旧结构S盒，确保设计算法具有更好的安全性能；新算法的解密过程与加密过程具有相同的迭代结构，因此加密和解密过程对称性好；基于耦合图像网格的分组图像加密算法不仅具有较好的安全性能，如密钥空间大、初始敏感性强，而且对损坏的密文图像有良好的恢复效果；同时，新算法对加密图像的规格尺寸没有相关限制，使算法更加实用。